Ecuaciones Cuadraticas

Las ecuaciones cuadráticas se dividen en dos:

Completas e Incompletas

Completas:
                   las completas son aquellas que traen la ecuación bien estructurada, tiene una con                      letra y exponente, y una con letra y una solo letra. EJEMPLO:

                              
Incompletas:    
                   Son aquellas que tienen un numero con exponente y una letra , o , las que tienen un exponente y                     una letra




                       

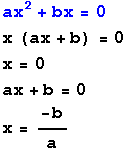
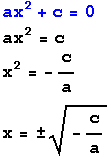
Las ecuaciones cuadráticas se resuelven por distintas soluciones de factorizacion

*FACTOR COMÚN
*TRINOMIO CUADRADO PERFECTO
*TRINOMIO DE SEGUNDO GRADO
*DIFERENCIA DE CUADRADOS

• FACTOR COMÚN

Número entero que divide exactamente a dos o más números dados sin dejar un residuo. Por ejemplo, tanto 3 como 6 son factores comunes de 6, 12 y 18. Ya que 6 es el número mayor que divide exactamente a los tres, se denomina máximo factor común.

*pasos para resolver una ecuación por factor común

1. sacar el minimo comun divisor
2. dividir el minimo comun entre los valore de la ecuacion
3. acomodarlas en la ecuacion

EJEMPLO

10x² + 5xy - 20x : (5x)(2x+1y-4) = 10x²+5xy-20y
 
el m.c.d es 5 y se agarra x por que es la letra que mas se repite y la menor, luego se dividen los numeros por el m.c.d

• TRINOMIO CUADRADO PERFECTO

Se llama trinomio cuadrado perfecto ala ecuación de 3 términos tal que, dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados.



En el trinomio cuadrado perfecto los términos cuadrados son siempre positivos, en cambio el término del doble producto puede ser negativo; en este caso debe ser negativo uno de los términos del binomio cuyo cuadrado es el trinomio dado, del ejemplo anterior tenemos:




Ambas son respuestas correctas.

• TRINOMIO DE SEGUNDO GRADO

EJEMPLO : 

x² + 3x + 2 = (x + 1).(x + 2)

Es un "trinomio", pero no es "cuadrado perfecto". Se puede factorizar buscando las "raíces" con la fórmula para resolver ecuaciones cuadráticas. Y se factoriza así: a.(x - x₁).(x - x₂).  En este ejemplo "a" es igual 1, entonces no lo ponemos.

• DIFERENCIA DE CUADRADOS

Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.
 EJEMPLO:
          x⁶ - 4 = (x³ + 2).(x³ - 2)
                      x³   2
                  x⁶ 
es también un cuadrado, es el cuadrado de x³. Ya que (x³)² es igual a x⁶

• PRESENTACIONES EN POWER POINT

http://www.slideshare.net/matematicasec29/ecuaciones-cuadraticas-56838?from_search=4
http://www.slideshare.net/matematicasec29/ecuaciones-cuadraticas-61013
http://www.slideshare.net/lorenacruzcastro/ecuaciones-cuadrticas-6152143?from_search=2
http://www.slideshare.net/gatowillia/casos-de-factorizacion-18148636?from_search=2
http://www.slideshare.net/Abnrito14/factor-comun?from_search=2
http://www.slideshare.net/rexr/trinomio-cuadrado-perfecto?from_search=1
http://www.slideshare.net/breid/factorizacion-2586883

• Aqui algunos videos que me ayudaron a buscar informacion

http://www.youtube.com/watch?v=MJEkXE0fi6M
http://www.youtube.com/watch?v=Zl8mRoTrQ_k
http://www.youtube.com/watch?v=LWyZSXsMAr8
http://www.youtube.com/watch?v=bTWL4sXE57U