La translacion es un movimiento en el plano de tal forma que a cada punto de la figura le corresponde un vector de translacion.
Una translacion es una isometria en el espacio euclidiano caracterizada por un vector de translacion.
Un translacion es una isometria en el espacio eucilideo caracterizada por un unvecto
 , tal que a cada punto P es el objeto o figura se le hace corresponder otro punto P, tal que:
, tal que a cada punto P es el objeto o figura se le hace corresponder otro punto P, tal que:
objetos trasladados, a las cuales deslizan según el vector. Dado el carácter de isometría para cualesquiera puntos P y Q se cumple la siguiente identidad entre distancias
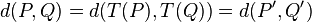
Más aún se cumple que
Notas:
- La figura trasladada es idéntica a la figura inicial.
- La figura trasladada conserva la orientación que la figura original.

Generalmete se usan coordenadas homogeneas para la translacon lineal sobre un espacio de dimensiones superiores, es diferente, ya que las figuras estan en diferemtes lados, pero el mismo dibujo ifente lado.
*Videos relacionados*
http://www.youtube.com/watch?v=Djt-VkgwPNE
http://www.youtube.com/watch?v=4UEzNcEFOmo
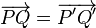
No hay comentarios:
Publicar un comentario