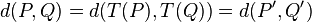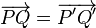Matematicas: febrero 2014

viernes, 14 de febrero de 2014

Tabulacion y Graficacion

Tabulación se refiere al hecho de calcular valores parciales para una función y compararlos en una tabla, de ahí el nombre de tabular.Ejemplo
sea f(x)=2x
Ya hemos visto como los modelos matemáticos nos ayudan a resolver desde los problemas más simples, hasta los problemas más complejos, también hemos visto que la complejidad o simplicidad de un modelo es el producto del trabajo intelectual y el estilo de resolver las cosas según la persona que lo aborda, sin embargo, todos buscan lo mismo al final del día, resolver un problema o buscar atender una necesidad.
Para atender el tema de tabular y graficar una función pensemos en una necesidad según el siguiente caso práctico:
El profesor responsable de las actividades de Protección Civil de ha solicitado a ti y a un conjunto de tus compañeros que pintes un círculo en el centro del patio para ahí colocar el punto de encuentro que es requerido como parte del proyecto de protección civil de la escuela.
Necesitas saber dos cosas para cumplir esta asignación.
Conocer el diámetro del círculo en base al radio que te solicitan tenga el círculo para que sea los suficiente mente grande y de esta forma que todos lo vean.

Saber los metros cuadrados de área para saber la cantidad de pintura que se necesita comprar (no es lo mismo pagar un cuarto de pintura, dos litros o veinte litros).

Donde x al igual que en la fórmula original representará el valor del radio.
Ahora vamos a tabular los resultados, esto significa obtener el valor numérico de la función al reemplazar posibles valores de x. Esta actividad es la misma que aprendiste cuando estudiamos el valor numérico de expresiones en la Unidad 1, sección 1-7.

Vamos a emplear herramientas más modernas, usemos Excel para obtener una tabla más completa y detallada haciendo incrementos más pequeños (del orden de 0.1) y que nuestra gráfica sea más exacta. Al momento de solicitar a Excel que ponga en el plano cartesiano los valores del área que obtuvimos nos queda una gráfica del siguiente tipo:

ecuaciones cuadraticas por formula general

Consideremos la ecuación general de segundo grado (ecuación cuadrática) que tiene la forma: $ax^{2}+bx+c=0$ .

Resolver esta ecuación implica encontrar el valor o los valores de $x$ que cumplen con la expresión, si es que existen.

Cuando nos enfrentamos por primera vez en la vida a esta clase de problemas, la primera forma en la que se intenta dar una respuesta es probando con varios números hasta "atinarle" (ya sea por que nos sonría la buena fortuna, o por aproximación).

Algunos incluso prueban número tras número hasta hallar la solución (Método de la "Fuerza Bruta").

Después, conforme nos vamos enfrentando a mas problemas que involucran ecuaciones cuadráticas, descubrimos algunos métodos de solución. De los primeros que aprendemos (por simplicidad) están el "Método Gráfico" (Realizar la gráfica correspondiente a la ecuación cuadrática igualada a cero y observar en que abscisas la gráfica "toca o pasa" por el eje horizontal del plano cartesiano). Otro método que aprendemos es el "Método de Factorización" (Trabajar con la expresión cuadrática igualada a cero hasta dejarla expresada como multiplicación de otras dos expresiones algebraicas, y encontrar "por simple observación" los valores que hacen que estas últimas dos ecuaciones sean iguales a cero).
Las desventajas de estos métodos es que implican trabajo excesivo, y no se garantiza que se encuentre la solución de la ecuación (al menos una solución "Real").

El último método que se estudia para resolver ecuaciones de segundo grado es la "Fórmula General".

$X_{1},_{2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

Analizando la raíz cuadrada, se llega a las siguientes conclusiones:

Si $b^{2}$ es menor que $-4ac$ los resultados de X serán dos valores con parte real y parte imaginaria. Es decir, el resultado sera un número complejo.

Si $b^{2}$ es mayor que $-4ac$ obtendremos dos valores distintos de X reales.

Y si $b^{2}$ es igual que $-4ac$ obtendremos dos valores de X reales e iguales.
Al término $b^{2}-4ac$ se le llama discriminante.

VIDEOS QUE ME AYUDARON

http://www.youtube.com/watch?v=Zl8mRoTrQ_k
http://www.youtube.com/watch?v=myQVK1QWR7o

jueves, 13 de febrero de 2014

Regla de la suma

Si dos eventos A y B son mutuamente excluyentes, esta regla indica que la probabilidad de que ocurra uno u otro de los eventos, es igual a la suma de sus probabilidades. P(A ó B) = P(A U B)P(A U B) = P(A)+ P (B)P(A ó B ó...ó Z) = P(A U B U...U Z)P(A U B U...UZ)= P(A)+ P(B) +... P(Z)REGLA GENERAL DE LA ADICIÓNCuando los eventos no son mutuamente excluyentes, la probabilidad de la ocurrencia conjunta de los dos eventos, se resta de la suma de las probabilidades de los dos eventos.P(A ó B) = P(A) + P(B) - P(A y B) En la teoría de conjuntos, la ocurrencia conjunta hace referencia a la intersección, por lo tanto:P(A y B) = P(A ∩B)Entonces: P(A U B) = P(A) + P(B) - P(A ∩ B)

¿Qué quiere decir esto?

Imaginad que tenéis una balanza en equilibrio:

Si colocamos el mismo peso en los dos platillos, la balanza seguirá en equilibrio:

Esto es lo que ocurre en las ecuaciones al aplicar la regla de la suma, si aumentamos o disminuimos la misma cantidad (" el mismo peso") en los dos miembros de la igualdad ("en los dos platillos de la balanza"), la igualdad sigue siendo cierta para el mismo valor de la incógnita, es decir obtenemos otra ecuación equivalente.

Por ejemplo, dada la ecuación:

x+5=14

Podemos sumar (-5) en los dos miembros obteniendo la ecuación equivalente que nos da la solución:

x+5-5=14-5

x=9

**videos que me ayudaron a hacer esta investigacion**

http://www.youtube.com/watch?v=d2M0qv-UMzA

http://www.youtube.com/watch?v=XwDWwmvEJUg

miércoles, 12 de febrero de 2014

Homotecia

Es la transformación geométrica que no tiene una imagen congruente, ya que a partir de una figura dada se obtienen una o va9ias figuras en tamaño mayor o menor que la figura dada, para obtenerlas se parte de un punto escogido arbitrariamente, al cual se llama centro de homotecia, del cual se trazan segmentos de recta, tantos como vértices tenga la figura que se va a transformar, se debe considerar otro elemento básico para desarrollar esta transformación, siendo esta una constante, la cual se denomina constante de homotecia que viene a ser la escala en la cual se realiza la reproducción.Tiene las siguientes propiedades:

Los ángulos de las figuras por homotecia son iguales ya que tienen la misma medida.

Los segmentos con paralelos.

Las dimensiones de dos figuras por homotecia son directamente proporciónales; esta proporción es fijada por la constante de homotecia.

Aquellas figuras que no cumplen con la propiedad de ser paralelos los segmentos se les denomina figuras semejantes, a las que cumplen con todas las propiedades se les denomina figuras homoteticas.
En una homotecia de centro el punto O y razón k:

Si k > 0, A y A′ están al mismo lado de O, y se dice que la homotecia es directa.

Si k < 0, A y A′ están a distinto lado de O, y se dice que la homotecia es inversa.

A la figura ABCD le hemos aplicado una homotecia de centro O y razón k, con k > 0; homotecia directa.A la figura ABC le hemos aplicado una homotecia de centro O y razón k, con k < 0; homotecia inversa.

*Algunos videos*

http://www.youtube.com/watch?v=DLXmtkmk1MI
http://www.youtube.com/watch?v=pKeqQaouwpU

*conclusion*
Bueno la homotecia directa es la que queda delante del punto y queda de la misma manera que la figura normal, en cambio la homotecia inversa queda del otro lado del punto y queda volteada del normal, se distinguen por ser la directa:positiva y la inversa:Negativa, si es -2 seria inversa y quedaria del otro lado del punto volteada y mas grande. si es 2 quedaria antes del punto mas grande e igual manera, si es 1 quedaria exactamente igual del lado positivo, y si es -1 queda de igual medidas pero del otro lado y volteados.

Simetria Central

Es cuando todas las partes tienen una parte correspondientes que esta a la misma distancia del punto central pero en la direccion opuesta.

se ve igual cuando lo mira desde direcciones opuestas, como izquierda VS derecha, o si se gira alrevez.
un ejemplo de la vida cotidiana es las cartas de pokar.

**Videos que me ayudaron*¨*

http://www.youtube.com/watch?v=msbjcIeRRGo
http://www.youtube.com/watch?v=RIsu_VvGlKQ

Simetria Axial

Decimos que una figura plana tiene simetría axial cuando podemos trazar una recta (llamada eje de simetría) que divida en dos partes la figura, de manera que si plegamos el plano por ese eje las dos partes coinciden. Observa que una parte "se refleja" en el eje para formar la otra, como si el eje actuase de espejo.

En esta actividad podrás dibujar figuras que tengan simetría axial, a partir del eje de simetría que la aplicación te mostrará. Solo tienes que mover el punto P (no lo confundas con P').

Es la simetria alrededor de un eje, de modo que un sistema tiene simetria axial o aximetria.
Dada una simetria se llama simetria axial de eje al movimiento que se transforma a un punto P a otro punto P' verificando que:

*El segmento Pp' es perpendicular a e

* Los puntos P' y p equisdistan del eje e

*videos que ayuden*

http://www.youtube.com/watch?v=FNSvDu_ENNg
http://www.youtube.com/watch?v=_7mac79KwKI

Translacion de Figuras

La translacion es un movimiento en el plano de tal forma que a cada punto de la figura le corresponde un vector de translacion.
Una translacion es una isometria en el espacio euclidiano caracterizada por un vector de translacion.
Un translacion es una isometria en el espacio eucilideo caracterizada por un unvecto ${\vec {u}}$ , tal que a cada punto P es el objeto o figura se le hace corresponder otro punto P, tal que:

${\begin{cases}T_{{\vec {u}}}:\mathbb{R} ^{n}\to \mathbb{R} ^{n}&\overrightarrow {PP'}={\vec {u}}\\P\mapsto P'=T(P)=P+{\vec {u}}\end{cases}}$

objetos trasladados, a las cuales deslizan según el vector. Dado el carácter de isometría para cualesquiera puntos P y Q se cumple la siguiente identidad entre distancias

$d(P,Q)=d(T(P),T(Q))=d(P',Q')\;$

Más aún se cumple que

$\overrightarrow {PQ}=\overrightarrow {P'Q'}$

Notas:

La figura trasladada es idéntica a la figura inicial.
La figura trasladada conserva la orientación que la figura original.

Generalmete se usan coordenadas homogeneas para la translacon lineal sobre un espacio de dimensiones superiores, es diferente, ya que las figuras estan en diferemtes lados, pero el mismo dibujo ifente lado.

*Videos relacionados*

http://www.youtube.com/watch?v=Djt-VkgwPNE

http://www.youtube.com/watch?v=4UEzNcEFOmo

martes, 11 de febrero de 2014

*ROTACIÓN DE FIGURAS

Es el movimiento de cambio de orientacion de una figura, desde un punto y moverla a un lado con el mismo punto.
puesto que a la rotacion se le llama Erroneamente, revolucion,devemos diferenciar estos terminos.
La rotacion de un cuerpo alrededor de un eje corresponde a un movimiento en el que distintos puntos del cuerpo presentan velocidades que son proporcionales a sus distancias de eje.
Un ejemplo muy claro es el de la rotacion de la tierra sobre su propio eje de rotacion, con un periodo de rotacion de un dia.

Conclusion:
Bueno pues a este tema si le agarre bien, bueno pues Rotacion sobre un punto determinado, cada figura gira dependiendo el punto y lo valores dados, esto puede darse en el lado negativo tanto en el positivo del plano cartesiano, a la figura original se la pone (ABC) y a la que se le copio se le pone (A'B'C'), este se menciona asi, A prima, B prima, C prima, como ya habia puesto un ejemplo de esto en la vida real es lo del planeta ya que gira sobre su propio eje, eso fue lo que ya le entendi :)

http://www.youtube.com/watch?v=OU9jjyL_sp0